Theoretical Studies
Theoretical study of disturbance evolution in parallel shear flows.
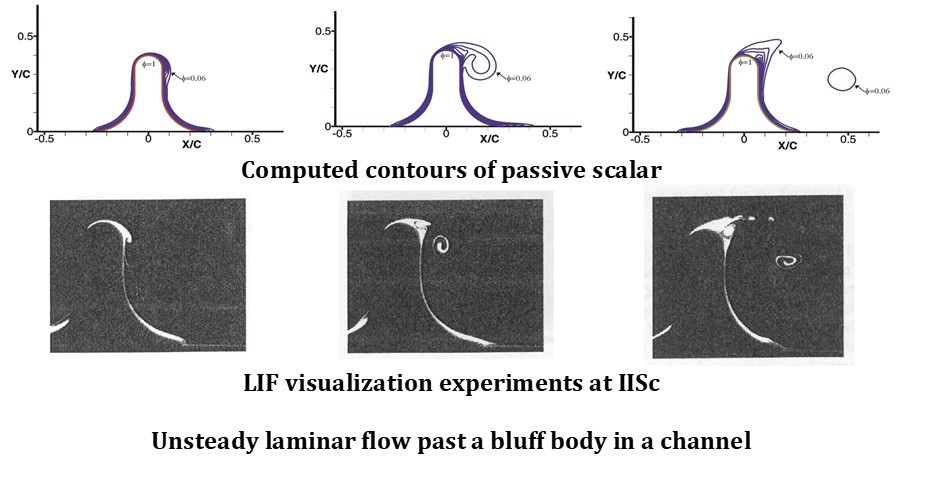
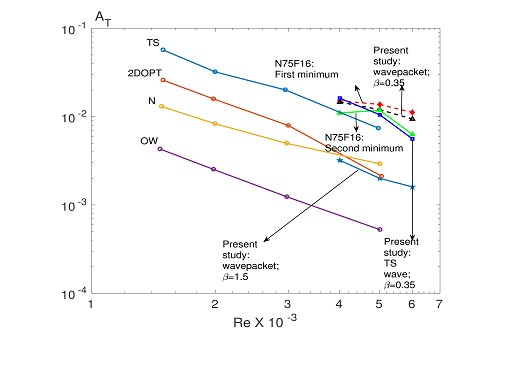
There have been numerous studies on the receptivity, transient growth and nonlinear development of disturbances in shear flows in general and plane Poiseuille flow (PPF) in particular. However, none of these tries to trace the disturbance evolution from the initial linear stage to fairly strong nonlinear stages. The disturbance evolution in PPF due to a localized disturbance source, for example a vibrating ribbon starting from the linear evolution stage to the secondary disturbance development regime has been studied. The analytic solution to the linear evolution problem for PPF shows emergence of a spatial Tollmien- Schlichting wave and a wave packet, unlike the earlier findings which show only the TS waves. Which of these two parts grows depends on the Reynolds number. A secondary stability analysis of the dominant part is seen to explain the disturbance growth observed in the seminal experiments of Nishioka, Iida & Ichikawa (J. Fluid Mech., vol.72, 1975, p.731) and Nishioka, Iida & Kanbayashi (NASA TM-75885, 1981). Threshold amplitudes for instability at a subcritical Reynolds number Re = 5000 are obtained from the time-averaged three dimensional disturbances, obtained by combining the secondary base states and the growing Floquet modes. The observed minima of the threshold amplitude curves in the experiments have been explained in terms of the instabilities of two different base states- the TS wave and a wave packet state. Computations, for another subcritical (4000) and a supercritical (6000) Reynolds number, have also been validated with the experimental data.
Dynamic coupling between sloshing and container motion under gravity
Sloshing in containers subject to a variety of motions, apart from being of theoretical interest, has numerous practical applications and has been studied for well over a hundred years. The slosh literature is replete with methods to determine the sloshing due to prescribed container motions. A few studies consider slosh interaction with elastic containers and also slosh interaction with support structures and tuned sloshing absorbers / liquid dampers. Motion of free bodies, ie. whose motion is a priori un prescribed, containing liquids is relatively less studied. A very simple example is the motion of a liquid-bearing rectangular container sliding down an inclined plane; how the sloshing affects the container motion is of interest. Presently, a linearized solution for a partially-filled sliding rectangular container, starting from rest has been obtained for small angles of inclination. It is interesting to note that, depending on the fill volume and the ratio of container-to-fluid mass, the container acceleration is significantly different from that of the rigid body acceleration and is time-dependent.
Movie I describes the sliding motion of a partially-filled rectangular container along a smooth plane of 8° inclination in a reference frame moving with acceleration due to gravity.
The initial boundary value problem (IBVP) and the solution methodology are presented in
S. Usha and R. Kidambi, The vibrating ribbon problem in plane Poiseuille flow., PD-CTFD/2017/1004.
The secondary stability analysis for the new base state, comprised of plane Poiseuille flow and wavepackets is presented in
R. Kidambi and S. Usha, Secondary instability of a wavepacket in plane Poiseuille flow., PD-CTFD/2017/1016.

 English
English हिन्दी
हिन्दी